Mohammad Sarraf Joshaghani's Codes

LimitedDG

— Code for the numerical solution of immiscible two-phase flows in porous media, which is obtained by augmenting interior penalty DG formulation with post-processing flux and slope limiters. Resulting solutions are accurate, robust, mesh-independent, mass-conservative, and maximum-principle satisfying. The repo entails several examples of pressure-driven flow and quarter-five spot that account for gravity, capillary effects, and heterogeneity.

Download from GitHub https://github.com/msarrafj/LimiterDG

References:

[1]

M. S. Joshaghani, B. Riviere, and M. Sekachev, Maximum-principle-satisfying discontinuous Galerkin methods for incompressible two-phase immiscible flow
submitted to Computer Methods in Applied Mechanics and Engineering Journal, 2021 [arXiv link] [Abstract] [BibTeX]

@article{joshaghani2021Incompressible,
  title={Maximum-principle-satisfying discontinuous Galerkin methods for incompressible two-phase immiscible flow},
  author={M.~S.~Joshaghani and B.~Riviere and M.~Sekachev},
  journal={arXiv preprint arXiv:2106.11807},
  year={2021}
}

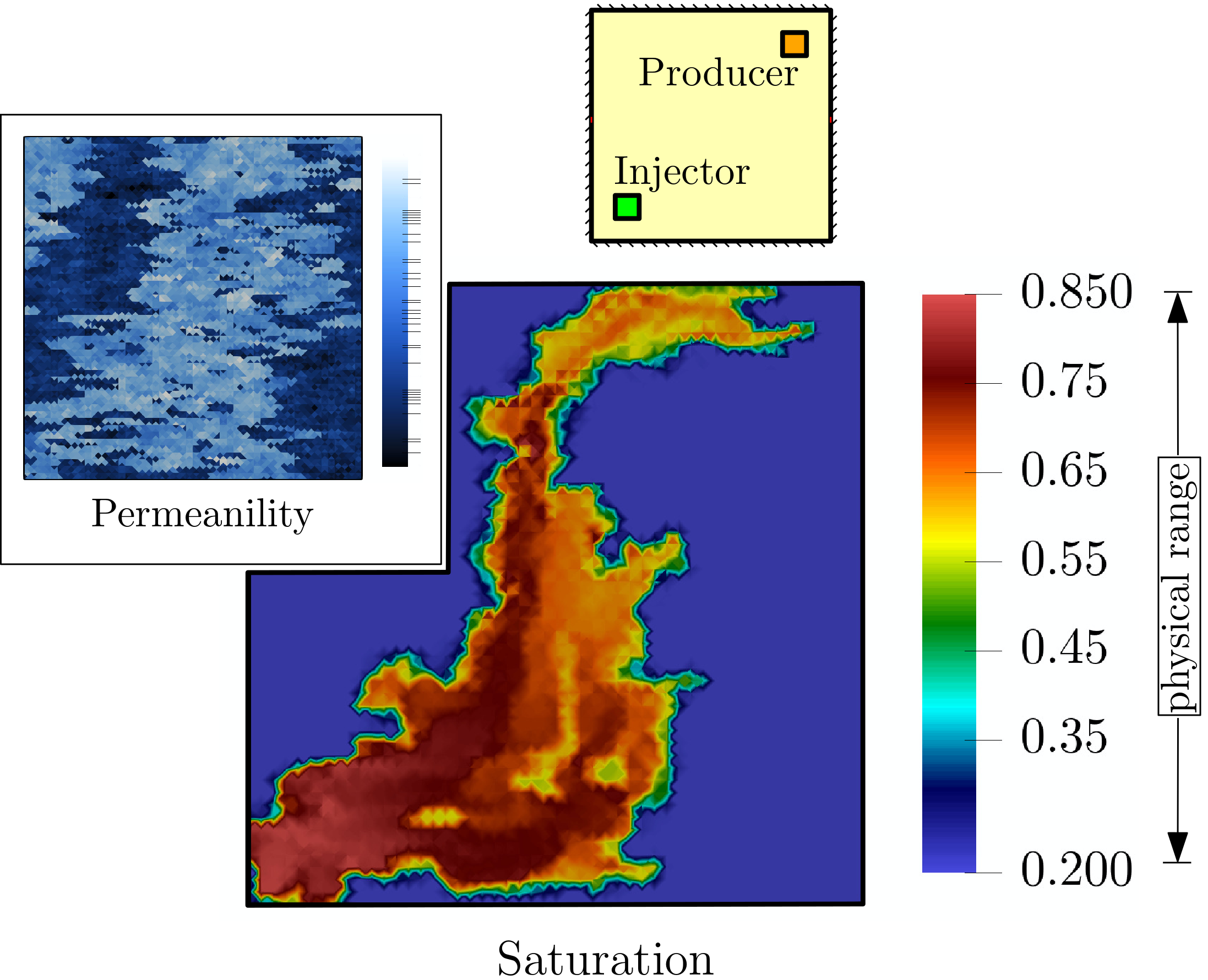
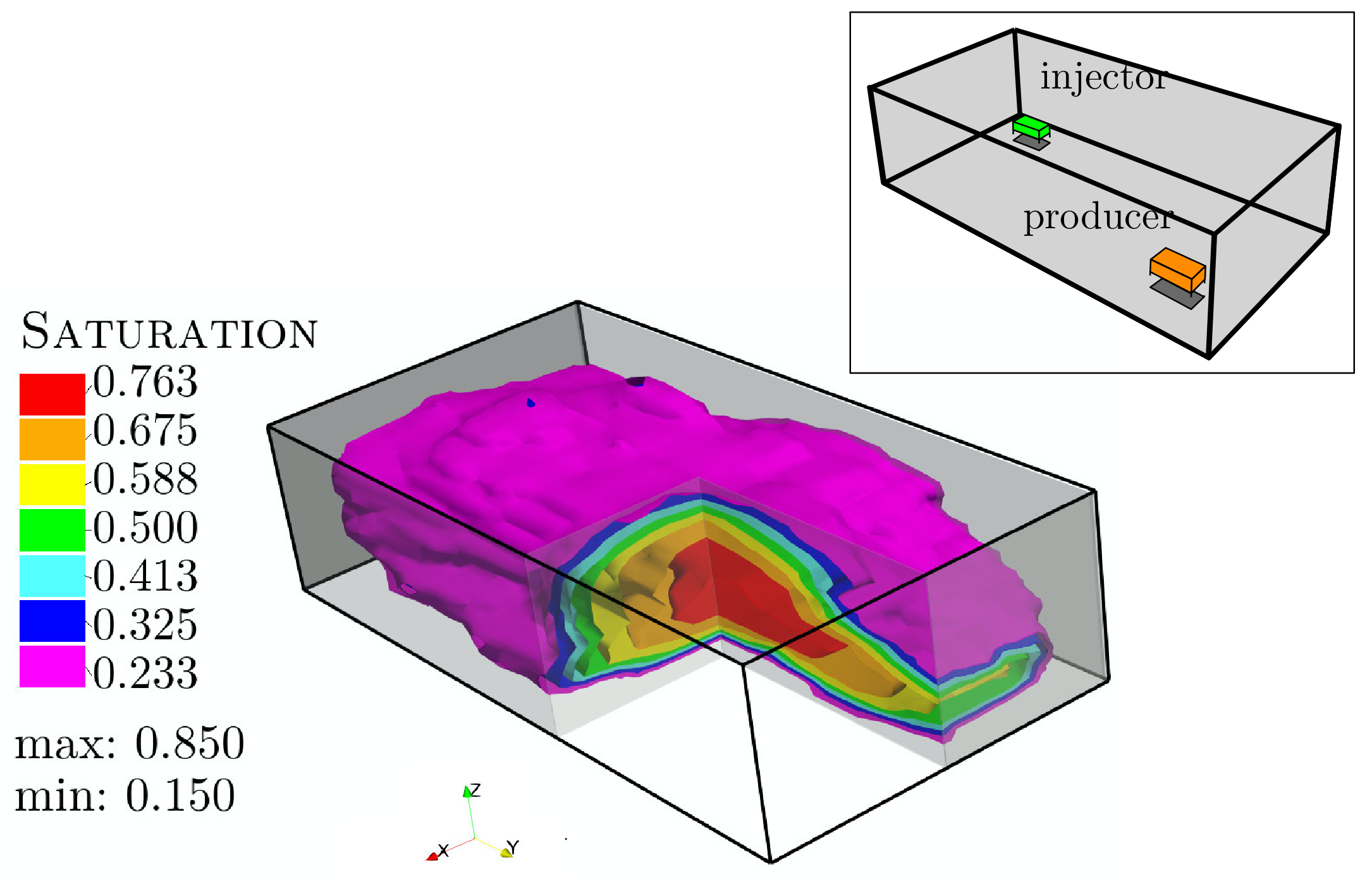
VertexBased-FE

— Code for a low-order numerical scheme that solves two-phase flows problems in heterogeneous porous media, The method is obtained by a first order finite element method equipped with mass-lumping and flux upwinding. The repo entails several examples of quarter-five spot problems and SPE10 problems in 2D and 3D settings.

Download from GitHub https://github.com/msarrafj/Vertex_based_method

References:

[1]

M. S. Joshaghani, V. Girault, and B. Riviere, A vertex scheme for two-phase flow in heterogeneous media
submitted to Journal of Computational Physics, 2021 [arXiv link] [Abstract] [BibTeX]

@article{joshaghani2021vertex,
  title={A vertex scheme for two-phase flow in heterogeneous media},
  author={M.~S.~Joshaghani and V.~Girault and B.~Riviere},
  journal={arXiv preprint arXiv:2103.03285},
  year={2021}
}

HPC-composableSolver

— Code for implementing recently developed block preconditioning strategies to solve the discrete systems that arise from double porosity/permeability model in 2D and 3D porous media. Implementation for three different finite element discretizations (classical mixed formulation with H(div) elements, stabilized continuous Galerkin mixed formulation, and stabilized discontinuous Galerkin mixed formulation) are provided to compare scalability of solver strategies for each case. Solvers are implemented seamlessly using the existing PETSc’s composable solver options.

Download from GitHub https://github.com/msarrafj/HPC_composableSolver

References:

[1]

M. S. Joshaghani, J. Chang, K. B. Nakshatrala, and M. G. Knepley, On composable block solvers and performance spectrum analysis for double porosity/permeability model
Journal of Computational Physic, 386: 428-466, 2019 [arXiv link] [Abstract] [BibTeX]

@article{joshaghani2019composable,
title={Composable block solvers for the four-field double porosity/permeability model},
author={M.~S.~Joshaghani and J.~Chang and K.~B.~Nakshatrala and M.~G.~Knepley},
journal={Journal of Computational Physics},
volume={386},
pages={428--466},
year={2019},
publisher={Elsevier}
}

[2]

M. S. Joshaghani, Multi-scale and interface mechanics for porous media: mathematical models and computational frameworks
PhD Thesis, University of Houston, 2019 [Abstract]

Abstract:
The are many challenges in subsurface modeling. First, many important subsurface processes occur at the interfaces, either the interface of two different porous media (e.g., layered media) or the interface of free-porous media (e.g., hyporheic zones, arterial mass transport). Second, these processes (flow, transport, and mechanical deformation) are complex, coupled, and multi-physics by nature. Third, natural geomaterials such as fissured rocks often exhibit a pore-size distribution with two dominant pore scales. Fourth, the practical problems are invariably large-scale by nature. Thus, successful modeling of such processes in complex porous media requires: (i) an accurate prescription of flow dynamics within each region and at the interface, (ii) development of robust and accurate computational methods, and (iii) implementation and understanding of these models in a parallel and scalable high-performance computing (HPC) environment.

This dissertation develops modeling strategies to advance the current state-of-the-art in subsurface modeling to address the challenges mentioned above. The specific aims are three-fold: First, we develop a comprehensive mathematical framework that provides a self-consistent set of conditions for flow dynamics at an interface. It will be shown that many of the popular interface conditions form special cases of the proposed framework. The approach hinges on extending the principle of virtual power to account for the power expended at the interface and then appealing to the calculus of variations.

Second, we present a discontinuous Galerkin formulation for the double porosity/permeability (DPP) model. We present a numerical procedure to discretize the interface conditions accurately. We develop numerical strategies to simulate and study the flow of fluids in porous media with complex pore-networks by using the DPP model. We also devise solver and parallel computing strategies to solve large-scale practical problems.

Third, we address the coupling of mechanical deformation of the porous solid with transport processes. We assume the porous solid to be an elastoplastic material, and transport of chemical species to be Fickian and develop a mathematical model and a robust computational framework. These modeling tools can be applied to a variety of problems such as moisture diffusion in cementitious materials and consolidation of soils under severe loading-unloading regimes.

[BibTeX]

@misc{SarrafPhD,
title = {Multi-scale and interface mechanics for porous media: mathematical models and computational frameworks},
author = {M.~S.~Joshaghani},
year = {2019},
institution = {University of Houston},
}

DPP-DG

— Code for a stabilized mixed DG formulation of double porosity/permeability (DPP) model, which describes the flow of a single-phase incompressible fluid in a rigid porous medium with two distinct pore-networks with possible mass transfer across them. The method provides accurate results even for disparate material properties, captures physical instabilities while eliminating numerical artifacts, and supports non-conforming discretizations. The repo entails codes for solving the coupled flow-transport problem (such as miscible displacement) in the heterogeneous porous medium.

Download from GitHub https://github.com/msarrafj/Double_Porosity_Permeability

References:

[1]

M. S. Joshaghani, S. H. Joodat, and K. B. Nakshatrala, A stabilized mixed discontinuous Galerkin formulation for double porosity/permeability model
Computer Methods in Applied Mechanics and Engineering Journal, 352: 508-560, 2019 [arXiv link] [Abstract] [BibTeX]

@article{joshaghani2019stabilized,
title={A stabilized mixed discontinuous Galerkin formulation for double porosity/permeability model},
author={M.~S.~Joshaghani and S.~H.~S.~Joodat and K.~B.~Nakshatrala},
journal={Computer Methods in Applied Mechanics and Engineering},
volume={352},
pages={508--560},
year={2019},
publisher={Elsevier}
}

[2]

M. S. Joshaghani, Multi-scale and interface mechanics for porous media: mathematical models and computational frameworks
PhD Thesis, University of Houston, 2019 [Abstract]

[BibTeX]

@misc{SarrafPhD,
title = {Multi-scale and interface mechanics for porous media: mathematical models and computational frameworks},
author = {M.~S.~Joshaghani},
year = {2019},
institution = {University of Houston},
}

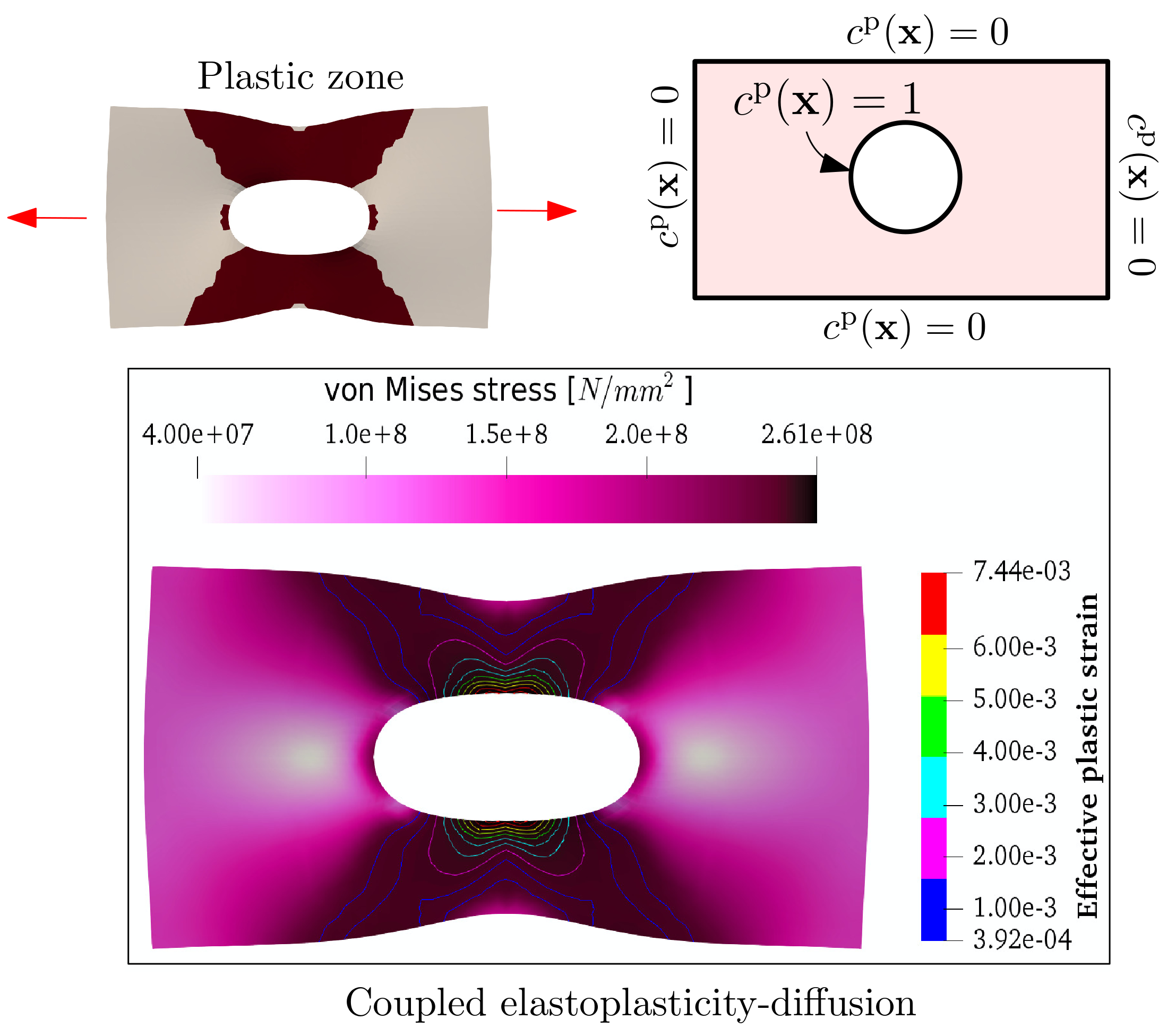
StableDegradation

— Code for diffusion-induced degradation/healing of solid materials that undergo (elastoplastic) deformation. Solver hinges on an optimization-based non-negative (NN) formulation that respects physical constraints. This code entails two different coupling strategies and two different degradation models.

Download from GitHub https://github.com/msarrafj/Coupled-plasticity-diffusion

References:

[1]

M. S. Joshaghani, and K. B. Nakshatrala, A modeling framework for coupling plasticity with species diffusion
submitted to International Journal for Numerical Methods in Engineering, 2020 [arXiv link] [Abstract] [BibTeX]

@article{joshaghani2020modeling,
  title={A modeling framework for coupling plasticity with species diffusion},
  author={M.~S.~Joshaghani and N.~B.~Nakshatrala},
  journal={arXiv preprint arXiv:2011.06652},
  year={2020}
}